CFD simulation of wet electrostatic scrubbers for the mitigation of dust in livestock buildings

Se-Woon Hong; Jinseon Park; Se-Yeon Lee; Kehinde Favour Daniel; Chae-Rin Lee; Ji-Yeon Park

doi:10.11109/JAES.2024.26.2.097

Preview

Research article

Journal of Animal Environmental Science. 30 August 2024. 97-104
https://doi.org/10.11109/JAES.2024.26.2.097

CFD simulation of wet electrostatic scrubbers for the mitigation of dust in livestock buildings

축산 시설 내 먼지 저감을 위한 습식 전기집진기의 전산유체역학 시뮬레이션

Se-Woon Hong¹⁴^*

Jinseon Park²

Se-Yeon Lee³⁴

Kehinde Favour Daniel³⁴

Chae-Rin Lee³⁴

Ji-Yeon Park³⁴

홍 세운¹⁴^*

박 진선²

이 세연³⁴

Daniel Kehinde Favour³⁴

이 채린³⁴

박 지연³⁴

¹ Professor, Department of Rural and Biosystems Engineering, Chonnam National University, 77 Yongbong-ro, Buk-gu, Gwangju 61186, Republic of Korea

²Research Professor, AgriBio Institute of Climate Change Management, Chonnam National University, 77 Yongbong-ro, Buk-gu, Gwangju 61186, Republic of Korea

³Graduate Student, Department of Rural and Biosystems Engineering, Chonnam National University, 77 Yongbong-ro, Buk-gu, Gwangju 61186, Republic of Korea

⁴Education and Research Unit for Climate-Smart Reclaimed-Tideland Agriculture (BK21 four), Chonnam National University, 77 Yongbong-ro, Buk-gu, Gwangju 61186, Republic of Korea

¹전남대학교 지역․바이오시스템공학과 교수

²전남대학교 기후변화대응농생명연구소 연구교수

³전남대학교 지역․바이오시스템공학과 대학원생

⁴BK21 기후지능형간척지농업교육연구팀

^{*Corresponding Author}

License (open-access, https://creativecommons.org/licenses/by-nc/4.0/):

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (https://creativecommons.org/licenses/by-nc/4.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

Effective dust removal in livestock facilities is crucial for maintaining air quality and protecting both animal and human health. This study investigated the performance of a conceptual wet electrostatic scrubber (WES) in removing dust particles (PM₁₀ and PM_2.5) from livestock facilities using a computational fluid dynamics (CFD) model. The CFD model was developed to understand the principles of the WES including corona discharge, water droplet charging in an electric field, electrostatic forces, and the dynamics of dust particles. The CFD results showed that the water droplet charge varied significantly with the electrode size and space charge density. As the water droplets were charged greatly, the dust removal efficiency was improved. In addition, the dust collection performance increased significantly when both water droplets and dust particles were charged negatively and positively, respectively. The findings emphasized that the acceleration of dust particles induced by the electrostatic forces must be sufficiently large to enhance the dust removal efficiency. The study demonstrated that the CFD simulations are effective for evaluating the WES performance and understanding the dust collection process.

Keywords

Corona discharge

Dust removal

Dust scrubber

Electrostatic forces

MAIN

서 론
재료 및 방법
1. 습식 전기집진기의 원리
2. 전산유체역학 모델
3. 습식 전기집진기의 평가
결과 및 고찰
1. 전극의 크기에 따른 물방울 전하 비교
2. 정전기력의 유무에 따른 집진 성능 비교
3. 습식 전기집진기의 추가 모델링
결 론

서 론

축산업은 전 세계적으로 중요한 식량 공급원으로서 사회 경제적으로 큰 역할을 하고 있다. 그러나 축산업은 다양한 환경 문제의 원인으로도 지목되며, 환경 문제를 개선하기 위한 다양한 노력들이 지속되어 왔다. 특히 축산 시설에서 배출되는 먼지(PM₁₀, PM_2.5 등)는 인근 지역의 대기질 악화와 주민들의 건강 문제를 유발할 수 있다 (Carotenuto et al., 2010; Wood and Van Heyst, 2016). 먼지에 흡착될 수 있는 악취 물질과 병원균 들은 먼지에 의해 장거리로 확산될 수 있어 주변 환경에 피해를 줄 수 있다 (Tan and Zhang, 2004). 또한 축산 시설 내의 고농도 먼지는 작업자의 작업 환경을 악화시킬 수 있고 가축들의 건강과 생산성에 악영향을 줄 수 있다 (Tan and Zhang, 2004). 따라서 축산업의 발전을 위해서는 축사에서 발생하는 먼지의 효과적인 저감 방법을 찾는 것이 시급한 과제이다 (Wood and Van Heyst, 2016).

축산 시설에서 먼지를 제거하기 위한 기술로는 사이클론 집진기와 필터 집진기, 건식 전기집진기 등이 있다 (Tan and Zhang, 2004; Wood and Van Heyst, 2016). 사이클론 집진기는 간단한 구조와 간편한 유지보수가 장점이지만 상대적으로 큰 입경의 먼지 입자보다 미세 먼지의 제거 효율이 낮은 단점이 있다. 필터를 이용한 집진기는 다양한 크기의 먼지에 대해 높은 제거 효율을 보이지만 주기적인 필터 교체를 위한 유지보수 비용이 크다는 단점이 있다. 정전기력을 이용한 건식 전기집진기는 사이클론 집진기에 비해 미세 먼지에도 높은 제거 효율을 보이지만, 먼지의 제거와 처리 과정에서 재비산의 문제가 발생하는 단점이 있다.

축산 시설에서의 먼지 저감을 위한 다양한 기술들이 개발되고 있지만, 그 중에서도 습식 전기집진기(Wet Electrostatic Scrubber)는 먼지의 저감에 있어 매우 효과적인 방법으로 주목받고 있다. 습식 전기집진기의 장점으로는 다양한 먼지 입자의 크기에 걸쳐 높은 제거 효율을 보이고 (Tan and Zhang, 2004; Carotenuto et al., 2010), 물을 사용하는 과정에서 먼지가 재비산되는 것을 방지할 수 있으며, 먼지뿐만 아니라 가스상 오염물질도 동시에 제거하는데 유리하다는 것이다 (Wood and Van Heyst, 2016). 반면, 단점으로는 물을 사용하여 먼지를 제거하는 과정에서 물 사용량이 증가하고 수처리 문제가 추가로 발생하며, 먼지 제거 과정에서 습도가 증가하면서 장비의 부식 문제가 발생할 우려가 있다 (Wood and Van Heyst, 2016). 또한 오존이나 산화물 등의 오염물질의 발생 가능성이 제기되기도 한다 (Wood and Van Heyst, 2016). 복잡한 장치로 인하여 최적 성능을 유지하기 위해서는 정교한 설계와 조작이 필요하다 (Ye and Domnick, 2003).

습식 전기집진기는 먼지를 포함한 공기가 지나가는 집진기 내에 살포된 물방울이 먼지와 충돌하여 세정하는 방식으로 먼지를 제거한다 (Jaworek et al., 2002; Carotenuto et al., 2010). 이때 살포되는 물방울과 먼지는 각각 음전하와 양전하로 대전되어 정전기력에 의한 인력을 통해 충돌 가능성을 높이는 원리이다. 습식 전기집진기의 효과적인 설계와 운용을 위해서는 물방울과 먼지에 대전되는 전기력, 입자들간의 정전기력에 의한 인력, 물방울과 먼지 입자들에 작용하는 힘들의 역학적인 관계와 입자들의 충돌과 이동 등 다양한 물리 역학적 현상에 대한 이해와 해석이 필요하다 (Jaworek et al., 2002; Manuzon, 2012).

전산유체역학 (CFD, computational fluid dynamics) 시뮬레이션은 이러한 정전기력과 입자들의 유체역학적 이동 현상에 대한 해석에 널리 사용되어 왔으며 높은 신뢰도를 보여 왔다 (Ye and Domnick, 2003; Geiling et al., 2012; Manuzon, 2012). 정전기력에 의한 입자의 이동, 입자간의 충돌에 의한 먼지 제거 과정 등 다양한 물리적 현상들을 통합적인 CFD 모델로 구현한다면, CFD 시뮬레이션은 복잡한 전기 장치의 구성과 계측을 대신하여 다양한 전기적 설계 조건에 따른 먼지 제거 효과를 체계적이고 효과적으로 예측할 수 있을 것이다.

본 연구의 목적은 습식 전기집진기를 CFD 모델로 구성하고 정전기력에 의한 먼지의 제거 과정을 연구하는데 있다. 습식 전기집진기의 작동 원리와 코로나 방전, 물방울의 전하, 정전기력에 의한 먼지의 역학적 이동과 제거 과정을 모의하고 분석하였다.

재료 및 방법

1. 습식 전기집진기의 원리

(1) 코로나 방전

코로나 방전(corona discharge)은 (-)고전압을 인가한 전극에서 음이온이 방출되는 현상을 의미한다. 음이온은 전극을 둘러싼 공기에 발생하고, 공기 중을 통과하는 물질에 대전되어 물질이 음전하를 띠게 한다. 코로나 방전은 전극 주변의 전기장이 전도 영역을 만들기에 충분히 높지만, 아크 방전을 일으킬 만큼 충분히 높지 않을 때 시작된다. 일단 코로나 방전이 발생하면, 도체를 둘러싼 얇은 이온화 층에서 생성된 전하가 주변 공기 중에 공간 전하를 형성한다.

전기장( $E$ )과 이온화 공간 전하 밀도( $ρ_{i}$ )는 각각 식 (1)과 (2)의 푸아송(Poisson) 방정식과 전하 연속방정식에 의해 지배된다 (Ye and Domnick, 2003; Nielsen and Andersson, 2009; Farnoosh, 2011; Manuzon, 2012).

(1)

\nabla^{2} Φ = - ρ_{i} ϵ_{0}

(2)

\nabla \cdot (K ρ_{i} \vec{E} + ρ_{i} \vec{u} - D_{i} \nabla ρ_{i}) = 0

여기서 𝛷는 스칼라 전위 (V), $ρ_{i}$ 는 이온화 공간 전하 밀도 (C m^-3), $ϵ_{0}$ 는 공기의 전기 유전율 (8.854 × 10^-12 C V^-1 m^-1 또는 C² s² kg^-1 m^-3), 는 이온의 이동도 (m² V^-1 s^-1), $\vec{E}$ 는 전기장의 세기 (V m^-1), $\vec{u}$ 는 공기 흐름의 속도 (m s^-1), $D_{i}$ 는 이온 확산 계수 (10 m² s^-1)이다.

연속방정식에서 이온의 이동 속도가 일반적인 공기 흐름 속도보다 두 자리 수 정도 더 빠르기 때문에 $\vec{u}$ 항은 무시할 수 있다 (Farnoosh, 2011). Farnoosh (2011)은 대전되어 음전하를 띈 입자들이 많아지면 공간 내 전하 밀도를 증가시켜 전위와 이온화 전하 밀도 분포를 변화시킬 수도 있으므로, 식 (1)의 푸아송 방정식을 수정할 필요가 있다고 제안하였다. 본 연구에서는 식 (1)의 기본적인 푸아송 방정식을 사용하지만, 추후 연구에서는 입자들의 대전 과정에서의 공간 전하의 변화도 고려할 필요가 있을 것이다.

전기장의 세기는 스칼라 전위의 기울기로 정의할 수 있다 (Ye and Domnick, 2003).

(3)

\vec{E} = - \nabla Φ

(2) 전기장에서의 물방울 전하

물방울은 전기장을 통과하여 이동하면서 정전기장 내의 이온 흐름에 노출됨에 따라 일정량의 전하를 얻게 된다. 물방울 입자가 얻을 수 있는 최대 전하는 포화 전하량으로 계산될 수 있다 (Manuzon, 2012).

(4)

Q_{s} = \frac{3 ϵ_{r}}{ϵ_{r} + 2} π ϵ_{0} d_{p}^{2} | \vec{E} |

여기서, $Q_{s}$ 는 물방울 입자의 포화 전하량 (C); $ϵ_{r}$ 은 공기의 상대 유전율 (1.000590, 무차원)이다.

물방울 입자는 두 가지 과정으로 음전하를 얻게 된다 (Manuzon, 2012). 실제 물방울 입자의 전하가 포화 전하보다 작을 때에는 전기장 내 이온과의 충돌에 의해 전기장 대전(field charging)이 일어난다. 반면, 실제 물방울 입자의 전하가 포화 전하보다 큰 경우에는 이온의 불규칙한 운동에 의한 확산 대전(diffusion charging)에 의해 음전하를 얻게 된다. 물방울 입자의 대전 속도는 다음과 같이 계산될 수 있다 (Farnoosh, 2011).

(5)

\frac{d Q_{c}}{d t} = \{\begin{cases} \begin{array}{ll} \frac{Q_{s}}{τ_{q}} {(1 - \frac{Q_{c}}{Q_{s}})}^{2} + \frac{2 π α ρ_{i} K κ_{B} T d_{p}}{e}, & Q_{c} < Q_{s} \end{array} \\ \begin{array}{ll} \frac{α}{4 τ_{q}} (Q_{c} - Q_{s}) \exp (\frac{e (Q_{s} - Q_{c})}{2 π ϵ_{0} κ_{B} T d_{p}}), & Q_{c} \geq Q_{s} \end{array} \end{cases}

여기서, $Q_{c}$ 는 물방울 입자의 실제 전하량 (C); $e$ 는 전자 전하로 1.6 × 10^-19 C; 𝛼는 모델 상수; $κ_{B}$ 는 볼츠만(Boltzmann) 상수로 1.38066 × 10^-23 J K^-1; $T$ 는 온도 (K); $τ_{q}$ 는 대전 시간 상수 (s)이다.

모델 상수와 실제 조건에서의 이온 이동도는 다음과 같이 계산된다.

(6)

α = \{\begin{cases} \begin{array}{ll} 1 & , e_{norm} < 0.525 \end{array} \\ \begin{array}{ll} \frac{1}{{(e_{norm} + 0.457)}^{0.575}}, & e_{norm} \geq 0.525 \end{array} \end{cases}

(7)

K = K_{0} \frac{P_{0}}{P} \frac{T}{T_{0}}

(8)

e_{n o r m} = \frac{e d_{p}}{2 κ_{B} T} | \vec{E} |

여기서, $K_{0}$ 는 표준 대기 조건에서의 이온의 이동도로서 0.00022 m² V^-1 s^-1; $P$ 와 $T$ 는 실제 조건에서의 압력(pa)과 온도(K); $P_{0}$ 와 $T_{0}$ 는 표준 대기 조건에서의 압력(1.013 × 10⁵ pa)과 온도(300 K)이다.

대전 시간 상수는 포화 전하량의 절반에 도달하는 시간으로서 다음과 같이 계산한다.

(9)

τ_{q} = \frac{4 ϵ_{0}}{K ρ_{i}}

(3) 정전기력과 먼지 입자의 운동

먼지 입자의 운동은 항력, 중력, 부력 및 정전기력 등 입자에 작용하는 힘들의 합력을 라그랑지안 관점으로 계산한다. 이 중 음전하를 띈 물방울로 인해 먼지 입자에 작용하는 정전기력은 다음과 같이 계산된다 (Jaworek et al., 2002; Jaworek et al., 2006).

(10)

\begin{aligned} F_{e} = & - \frac{Q_{p} Q_{c}}{4 π ϵ_{0} r^{2}} + \frac{R_{p} Q_{c}^{2}}{4 π ϵ_{0} r^{3}} \frac{ϵ_{p} - 1}{ϵ_{p} + 2} (\frac{r^{4}}{{(r^{2} - R_{p}^{2})}^{2}} - 1) \\ + \frac{R_{c} Q_{p}^{2}}{4 π ϵ_{0} r^{3}} \frac{ϵ_{c} - 1}{ϵ_{c} + 2} (\frac{r^{4}}{{(r^{2} - R_{C}^{2})}^{2}} - 1) \end{aligned}

여기서, $Q_{p}$ 는 먼지 입자의 전하량 (C); $ϵ_{c}$ 와 $ϵ_{p}$ 는 각각 물방울과 먼지입자의 상대 유전율이며, $ϵ_{c}$ =80.1 (20℃에서)이고 PM₁₀과 PM_2.5에 대한 $ϵ_{p}$ =3.8~30 (Geiling et al., 2012); $r$ 은 물방울 입자와 먼지 입자의 중심 간 거리 (m); $R_{c}$ 와 $R_{p}$ 는 각각 물방울 입자와 먼지 입자의 반경 (m)이다.

2. 전산유체역학 모델

(1) 습식 전기집진기의 구조와 모델링

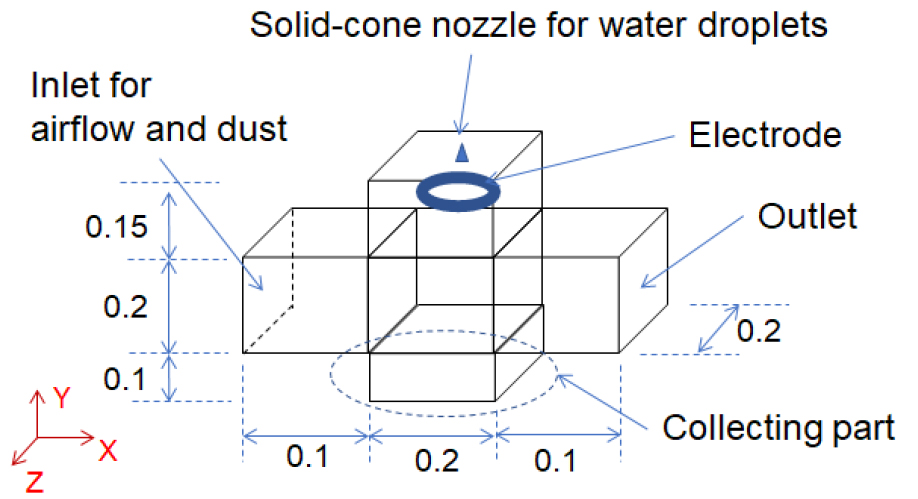
CFD 모델링을 위하여 가상의 습식 전기집진기를 구상하였다. Figure 1은 습식 전기집진기의 구조 형태와 크기를 나타낸다. 먼지를 동반한 공기는 입구에서 출구까지 x 방향으로 흐른다. 물방울은 가운데 구역의 상단에 위치한 solid-cone 노즐에서 분사된다. 노즐 아래에 위치한 전극이 전기장을 생성하며, 전극을 통과하는 물방울들은 음전하를 띠게 된다. 먼지 입자는 입구를 통해 전기집진기로 들어오며, 가운데 구역에서 물방울과 충돌한다. 물방울은 집진기 하단에 위치한 집수 부분에 도달하며, 물방울과 충돌하지 않은 먼지 입자들은 출구를 통해 집진기를 벗어나게 된다.

https://cdn.apub.kr/journalsite/sites/jaes/2024-026-02/N0360260205/images/jaes_26_02_05_F1.jpg

Figure 1.

Schematic model of the structure of WES (unit: m).

CFD 모델의 격자는 ICEM-CFD (ver. 18.2, Ansys Inc., Canonsburg, PA, USA)를 사용하여 생성하였으며, 계산은 Fluent (ver. 18.2, Ansys Inc., Canonsburg, PA, USA)를 사용하였다.

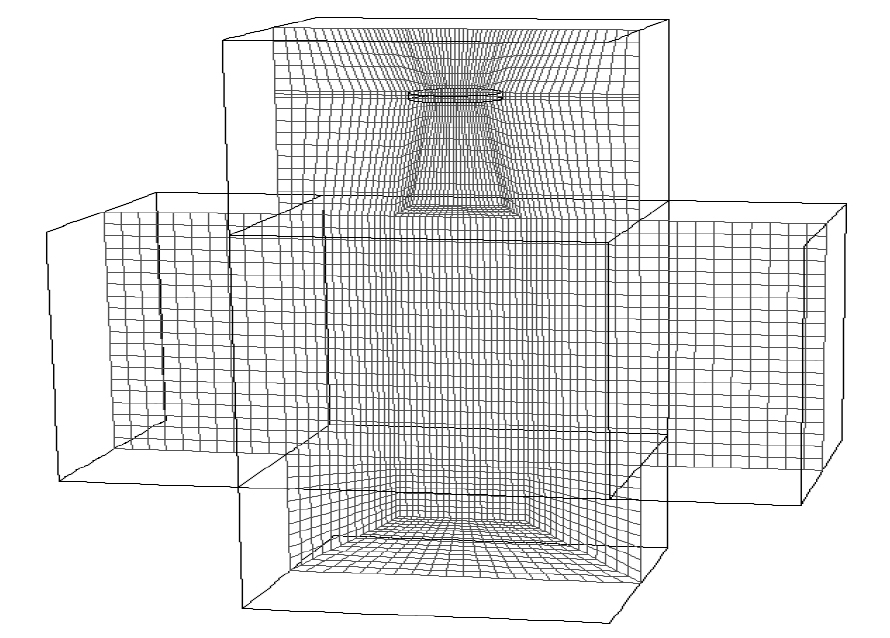
계산 영역은 평균 크기 0.01m의 99,760개의 육면체 셀을 정렬격자 형태로 메쉬를 생성하였다. 원형 고리 형태의 전극과 가운데 구역은 물방울의 세부적인 움직임과 먼지 입자와의 충돌을 시뮬레이션하기 위해 충분히 작게 설계되었으며, 최소 크기는 0.00186m이다 (Figure 2).

https://cdn.apub.kr/journalsite/sites/jaes/2024-026-02/N0360260205/images/jaes_26_02_05_F2.jpg

Figure 2.

Mesh generation on the plane at z=0.

(2) 세부 모델과 경계조건

CFD 모델은 비정상상태의 Reynolds-Averaged Navier-Stokes 방정식을 사용하여 공기의 기류를 해석하였다. 난류 인자들은 SST k-omega 모델을 사용하여 해석하였다. 시간 간격은 0.0001초로 충분히 작게 하여 물방울과 먼지의 충돌을 모의하고자 하였다. 먼지 입자는 PM₁₀과 PM_2.5로 정하였다. 물방울과 먼지 입자들은 Discrete phase model (DPM)을 사용하여 모의하였으며, Unsteady particle tracking을 활성화하여 공기 기류 해석과 동일한 시간 간격으로 비정상상태로 이동을 모의하였다. 이와 동시에 Virtual mass force와 Two-way turbulence coupling을 적용하여 현실적인 움직임에 가깝도록 해석하였다. 각 모델들의 세부사항들은 Ansys (2018)에 제시되어 있다. 추가적인 인자들의 설정값은 Table 1에 제시하였다.

Table 1.

Parameters for WES system.

Parameters	Values
Electricity input on electrode	12 kV
Space charge density at electrode surface	0.09 mC m^-3
Dust particle charge	+0.68 mC kg^-1
Diameter of water droplets	150 μm
Water flow rate	0.00378 kg s^-1
Dust mass flow rate	4 × 10^-7 kg s^-1 (PM₁₀) 5 × 10^-8 kg s^-1 (PM_2.5)
Dust particle density	600 kg m^-3

입구에서 바람의 유속은 1 m s^-1로 설정하였으며, 먼지 입자들은 0.0005초 동안만 유입되도록 하여 총 500개의 PM₁₀과 5000개의 PM_2.5가 집진기 내로 유입되었다. 유입되는 먼지 입자들은 Almuhanna and Maghirang (2010)가 돈사의 공기 중 먼지에서 측정한 결과에 따라 +0.68 mC kg^-1의 양전하를 띠는 것으로 가정하였다. 물방울은 20° 각도의 solid-cone 노즐에서 20 m s^-1의 초기 속도로 분사되도록 하였다. 물방울의 직경은 150 μm에 대해 모의하였다. 0.00378 kg s^-1의 유량으로 분사한 경우, 공기 중 1 $c m^{3}$ 에 약 500개의 물방울이 분포하게 된다. 입구와 출구 및 벽체에서의 공기 유동, 정전기력, DPM 입자들의 경계조건은 Table 2에 제시하였다.

Table 2.

Boundary conditions of CFD model.

Boundaries	Air flow	Electric potential	Space charge density	Particle
Inlet (Velocity inlet)	$\vec{u} = 1 \vec{i}$ (m s^-1)	$Φ = 0$	$ρ_{i} = 0$	Reflect
Outlet (Pressure outlet)	$P = 0$	$\frac{\partial Φ}{\partial x} = 0$	$\frac{\partial ρ_{i}}{\partial x} = 0$	Escape
Electrode (Wall)	$\vec{u} = 0$	$Φ = 12$ (kV)	$ρ_{i} = 0.09$ (mC m^-3)	Reflect
Collecting parts (Wall)	$\vec{u} = 0$	$\frac{\partial Φ}{\partial x} = 0$	$\frac{\partial ρ_{i}}{\partial x} = 0$	Trap
Walls around the electrode (Wall)	$\vec{u} = 0$	$\frac{\partial Φ}{\partial x} = 0$	$ρ_{i} = 0$	Reflect

(3) 물방울과 먼지 입자의 충돌

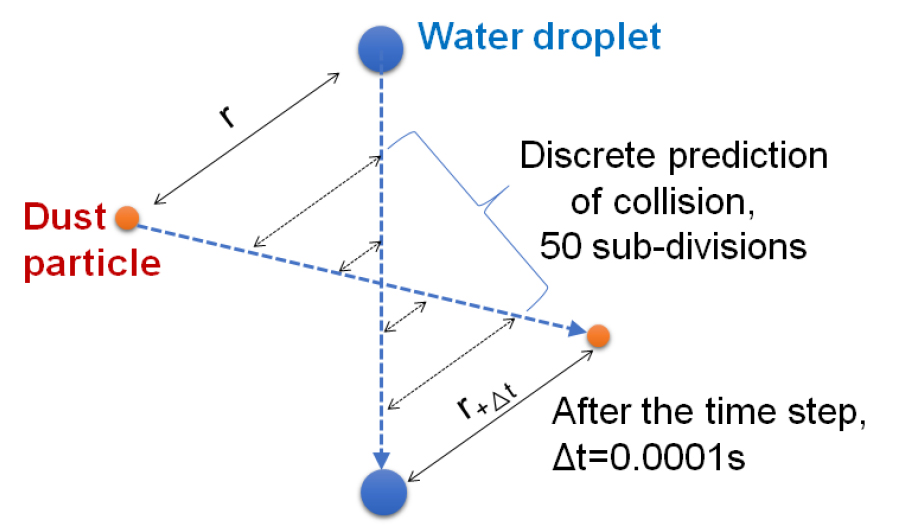
먼지 입자와 물방울이 한계 거리 내에 가까워지면 서로 충돌하는 것으로 간주하였다. 입자의 이동은 0.0001초 단위로 추적되는데, 이는 매우 작은 시간이지만 입자들의 크기를 고려하면 충분히 큰 시간이다. Figure 3은 이러한 예를 보여준다. 서로 일정 거리에 떨어져 있는 먼지 입자와 물방울이 물리적으로 서로 충돌할 수 있지만, 0.0001초 이후에는 서로를 지나쳐 여전히 일정 거리 떨어져 있을 수도 있다. 물론 0.0001초 보다 더 작은 시간 단위에서는 충돌이 감지될 수 있지만 전체적인 연산 시간과 비용이 크게 증가할 수 있다. 이에 대한 해결책으로, 시간 단위를 0.0001초로 유지하는 대신 User-defined functions (UDFs)를 개발하여 충돌 가능성을 감지하였다. 충분히 가까이 위치한 물방울과 먼지 입자에 대하여 0.0001초 이후의 입자들의 위치까지를 50개의 하위 시간 단계로 나누어 충돌 여부를 결정하였다. 50개의 하위 시간 단계에서는 공기 흐름 및 입자 추적에 대한 CFD의 지배 방정식을 계산하지 않기 때문에 계산 부담을 줄일 수 있다. 계산 상의 오차를 고려하여 물방울과 먼지 입자와의 거리가 ( $2 R_{p} + R_{c}$ ) 이내이면 충돌한 것으로 가정하였다.

https://cdn.apub.kr/journalsite/sites/jaes/2024-026-02/N0360260205/images/jaes_26_02_05_F3.jpg

Figure 3.

Collision detection through estimation of particle positions in 50 sub-time steps.

(4) CFD 시뮬레이션 수행 방법

습식 전기집진기의 시뮬레이션을 위해 수행해야할 주요 계산은 코로나 방전, 공기 흐름, 먼지 입자와 물방울의 충돌의 세 가지이다. 이 세 과정은 결합된 방식으로 커플링하여 해석하면 문제의 복잡성을 증가시키고 막대한 계산 자원을 필요로 한다. 따라서 본 연구에서는 세 가지 과정이 서로 간섭하지 않는다고 가정하고 세 과정을 순차적으로 해석하였다. Farnoosh(2011)에 따라 코로나 전하 방정식의 $\vec{u}$ 항은 무시할 수 있으므로, 코로나 방전과 공기 흐름은 서로 독립적으로 해석할 수 있다. 마찬가지로, 공기 중의 먼지 입자의 이동은 공기 흐름에 영향을 미치지 않으므로, 위의 가정은 타당하다.

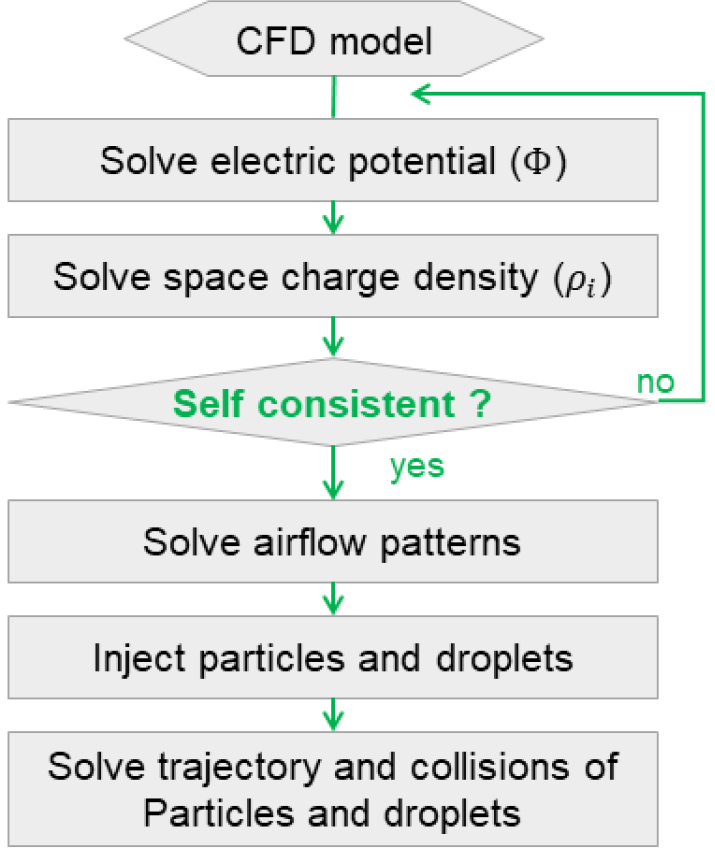
CFD 시뮬레이션의 계산 순서는 Figure 4와 같다. 먼저 전위 𝛷에 대한 지배 방정식을 계산하고, 공간 전하 밀도 $ρ_{i}$ 에 대한 지배 방정식을 계산하다. 다음으로 계산 결과가 일관성있게 수렴될 때까지 위 과정을 반복한다. 이후 도메인 내의 공기 흐름을 계산하고, 먼지 입자와 물방울을 주입한다. 비정상상태로 입자들의 이동을 모의하며, 먼지 입자와 물방울의 충돌을 탐지한다.

https://cdn.apub.kr/journalsite/sites/jaes/2024-026-02/N0360260205/images/jaes_26_02_05_F4.jpg

Figure 4.

Solution strategies for CFD simulations.

3. 습식 전기집진기의 평가

습식 전기집진기의 먼지 제거 가능성을 평가하기 위하여 Table 3과 같이 시뮬레이션 케이스를 정하였다. 이를 통해 정전기력의 유무, 전극의 크기가 먼지 제거 성능에 미치는 영향을 비교하였다. 또한 시뮬레이션 케이스의 결과로부터 먼지 제거 가능성을 높이기 위한 방법을 모색하였다.

Table 3.

Simulation cases for WES performance test.

Variables	Cases
Electrode radius	2 (0.05 m / 0.025 m)
Electrostatic force	3 (uncharged water, uncharged dust, all charged)

결과 및 고찰

1. 전극의 크기에 따른 물방울 전하 비교

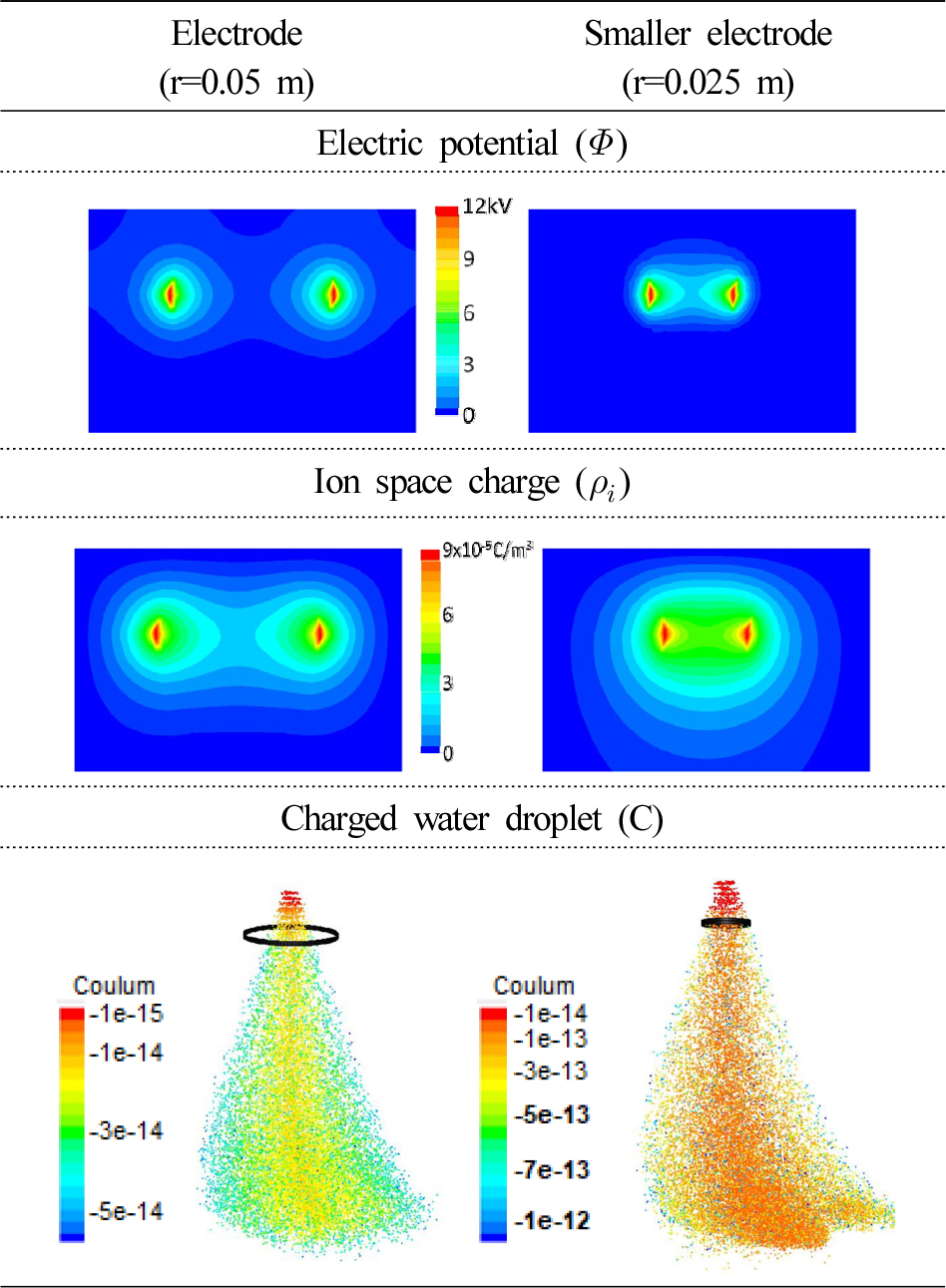
원형 전극을 통과한 물방울들은 이온을 흡수하여 Figure 5와 같이 음전하를 띠게 된다. 전기장은 전극으로부터의 거리에 따라 감소하므로, 전극 근처에서는 강하고 전극의 중간에서는 약하다. 따라서 전극 근처를 통과하는 물방울은 더 많이 대전되어 높은 음전하를 띠게 되고, 전극의 중앙을 통과하는 물방울은 적게 대전되어 낮은 음전하를 띠게 되었다. CFD 시뮬레이션 결과는 물방울이 전극에 의해 생성된 전기장을 통과하면서 서로 다른 수준으로 대전됨을 명확히 보여준다.

https://cdn.apub.kr/journalsite/sites/jaes/2024-026-02/N0360260205/images/jaes_26_02_05_F5.jpg

Figure 5.

Spatial distribution of electric potential, ion space charge and water droplets charged negatively by the electrode.

전극의 반경이 0.05 m 인 경우 -5e-14에서 -1e14 C 정도로 대전되었으며, 전극의 반경이 0.025 m 인 경우 -1e-12에서 -1e-13 C 정도로 대전되었다. 이는 물방울의 직경을 고려하여 환산 시, 각각 0.028 ~ 0.0057 mC kg^-1과 0.57 ~ 0.057 mc kg^-1로 변환된다. Pilat et al. (1974)은 습식 전기집진기 내에서 50 µm 물방울이 0.56 mC kg^-1의 음전하로 대전된 결과를 보였으며, 이와 비교할 때 0.025 m 반경의 전극을 사용하는 것이 현실적인 물방울의 전하 조건을 모의하는데 더 타당할 것이다.

2. 정전기력의 유무에 따른 집진 성능 비교

정전기력이 먼지의 제거에 미치는 영향을 분석하기 위하여 Table 4와 같이 물방울에 전하를 가하지 않은 상태 (Uncharged water), 먼지가 양전하를 띠지 않은 상태 (Uncharged dust), 먼지가 양전하를 띠고 물방울에 음전하를 가한 상태 (All charged)에 대하여 먼지 입자들의 제거 효율을 비교 분석하였다.

Table 4.

Dust removal performance according to the electrostatic forces.

Variables	Uncharged water	Uncharged dust	All charged
PM₁₀ injected	500
PM₁₀ removed	426	429	490
PM₁₀ removal efficiency	85.2%	85.2%	98.0%
PM_2.5 injected	5000
PM_2.5 removed	3937	3937	4080
PM_2.5 removal efficiency	78.7%	78.7%	81.6%

PM₁₀과 PM_2.5 모두 ‘Uncharged water’와 ‘Uncharged dust’ 상태에서는 동일한 먼지 제거 효율이 나타났다. 이는 물방울이나 먼지에 전하가 가해지지 않은 상태에서는 정전기력에 의한 입자 충돌이 없으며, 습식 전기집진기는 일반적인 습식 집진기와 동일하게 작동함을 의미한다. 반면 물방울과 먼지 입자가 모두 각각 음전하와 양전하를 띠는 경우에는 두 입자 간의 정전기력에 의한 충돌에 의해 먼지의 제거 효율이 상승하는 것으로 나타났다. 또한 CFD 모델로 이러한 습식 전기집진기의 먼지 제거 과정을 모의하는 것이 가능함을 보여준다.

전반적인 제거 효율은 PM₁₀이 PM_2.5보다 높게 나타났다. Wood and Van Heyst (2016)가 조사한 다양한 연구들에서도 PM_2.5의 제거 효율은 10~86%인데 반하여, PM₁₀의 제거 효율은 36~84%, 총 부유 분진(total PM)은 43~90%의 높은 제거 효율을 보이고 있다. 따라서 먼지 입자의 크기가 커질수록 제거 효율이 점차 커진다고 볼 수 있다. 한편, 본 연구에서는 정전기력이 없는 상태에서도 PM₁₀은 85.2%, PM_2.5는 78.7%의 비교적 높은 제거 효율을 보이고 있다. 이는 살포된 물방울이 공기 중 1 $c m^{3}$ 당 약 500개에 달하는 높은 밀도로 존재하기 때문으로 판단된다. 이에 따라 정전기력이 가해진 경우에는 PM₁₀과 PM_2.5의 제거 효율은 각각 98.0%와 81.6%로 높은 수준으로 증가하였음에도 단순한 습식 상태와 비교하여 큰 증가를 보이지는 않았다. 단, 정전기력에 의한 먼지의 제거 과정이 분명히 나타난 만큼, 공기 중에 분사되는 물의 양이 감소한다면 정전기력에 의한 효과가 더 분명히 나타날 것이다.

3. 습식 전기집진기의 추가 모델링

앞선 CFD 시뮬레이션에서 습식 전기집진기의 먼지 제거 과정이 효과적으로 모의되었다. 특히, 먼지 입자와 물방울의 결합 과정에서 정전기력의 영향이 명확히 나타났다. 하지만, 앞서 제시된 시뮬레이션의 조건들은 먼지의 제거 과정에 우호적인 상황이다. 물방울의 크기가 작고 분사량이 높아서 정전기력이 없이도 높은 제거 효율이 나타나고 있다. 따라서 먼지의 제거에 불리한 상황을 모의하여 정전기력의 영향을 살펴보고자 하였다.

물방울과 먼지 입자의 관성 충돌을 약화시키기 위하여 유입구의 공기 유속을 1.0 m s^-1에서 0.3 m s^-1로 감소시켰다. 물방울의 분사 속도 또한 20 m s^-1에서 5 m s^-1로 감소시켰다. 물방울의 직경은 150 µm에서 1,000 µm로 크게 증가시켰다. 물방울의 분사 유량은 0.004032 kg s^-1로 유사한 수준으로 유지시켜, 공기 중의 물방울 수가 적어지도록 조정하였다. 물방울과 먼지 입자의 충돌 조건은 두 입자의 거리기준을 ( $2 R_{p} + R_{c}$ )에서 ( $R_{p} + R_{c}$ )로 감소시켜 물리적인 충돌 시 실제로 충돌하는 것으로 더 엄격하게 변경하였다. 유입구에서의 먼지 입자의 유입되는 개수는 PM₁₀ 800개와 PM_2.5 5,200개로 조정하였다.

변경된 조건에서 수행한 CFD 시뮬레이션의 결과는 Table 5에 나타나 있다. 물방울에 전하를 가하지 않은 상태에서의 먼지 제거율은 PM₁₀ 27.3%, PM_2.5 28.8%로 나타났으며, 물방울에 전하를 가하면서 먼지 제거율은 PM₁₀ 30.8%, PM_2.5 30.5%로 약간 상승하였다. 하지만 하전된 물방울에 의한 먼지 제거 효율은 여전히 하전되지 않은 물방울과 비교하여 크게 개선되지 않았다. 충돌 시의 먼지 입자의 속도가 물방울의 전하에 따라 0.306 m s^-1에서 0.308 m s^-1로 상승한 것으로 보아 먼지 입자가 물방울의 전기력에 의해 끌리는 것은 명확하였다. 하지만 5 m s^-1의 속도로 하강하는 물방울을 따라잡아 물방울에 충돌하기에는 전기력에 의한 가속력이 충분하지 않은 것으로 판단되었으며, 이러한 이유로 정전기력에 의한 먼지 제거 효과가 크게 개선되지 않은 것으로 판단되었다.

Table 5.

Further investigation of dust removal performance with modified CFD simulations.

Variables	Uncharged water	All charged	All charged with greater electrostatic force
PM₁₀ injected	800
PM₁₀ removed	218	246	721
PM₁₀ removal efficiency	27.3%	30.8%	90.1%
PM_2.5 injected	5200
PM_2.5 removed	1499	1588	2631
PM_2.5 removal efficiency	28.8%	30.5%	50.6%
PM₁₀ Velocity at collection (m s^-1)	0.306 ± 0.028	0.308 ± 0.030	13.828 ± 5.748
PM_2.5 Velocity at collection (m s^-1)	0.307 ± 0.026	0.308 ± 0.025	2.299 ± 2.122

이를 개선하기 위하여 물방울과 먼지 입자 간의 정전기력을 임의로 1,000배 증가시켜서 CFD 시뮬레이션을 수행하였다. 그 결과 먼지 제거율은 PM₁₀ 90.1%, PM_2.5 50.6%로 크게 증가하였다. 충돌 시의 먼지 입자의 속도도 먼지 제거율은 PM₁₀ 13.8 m s^-1, PM_2.5 2.3 m s^-1로 크게 증가하여 정전기력에 의한 먼지 입자의 유인 효과가 원활히 작용한 것으로 나타났다. 이러한 결과들은 입자들의 전하를 통한 정전기력이 충분히 크고 이에 따른 입자의 유인 가속도가 충분히 커야 전기집진기 시스템이 효과적으로 작동할 수 있음을 보여준다. 정전기력은 전극의 전압이나 전극의 크기와 위치 등을 조정하여 증가시킬 수 있을 것이며, 이에 대한 후속 연구가 필요할 것이다.

결 론

본 연구에서는 습식 전기집진기를 CFD 모델로 구성하고 먼지 제거 과정을 평가하기 위하여 시뮬레이션을 수행하였다. 습식 전기집진기의 작동 원리와 코로나 방전, 전기장에서의 물방울 전하, 정전기력 및 먼지 입자의 운동을 분석하고, 최종적인 먼지 입자의 제거 과정을 모의하였다. 본 연구를 통한 주요 결론은 다음과 같이 도출되었다.

전극의 크기에 따라 물방울의 전하량이 크게 달라졌다. 전극의 반경을 작게하여 공간 전하 밀도를 높이면 물방울이 더 높은 음전하를 띠어 먼지 제거 효율이 높아졌다.

물방울이 음전하로 대전되는 것과 더불어 먼지가 양전하를 띠는 것이 중요하다. 물방울과 먼지가 모두 전하를 띠는 경우 집진 성능이 크게 증가하였다.

습식 전기집진기 내에서 물방울과 먼지의 정전기력에 의한 먼지의 유인 가속도가 충분히 커야 먼지 입자의 제거 효율을 증가시킬 수 있다

본 연구는 CFD 시뮬레이션이 습식 전기집진기의 성능을 평가하고 집진 과정을 이해하는데 효과적으로 활용될 수 있음을 보여주고 있다. 또한, 실험을 통해 충분한 검증을 거친다면 습식 전기집진기의 성능을 향상시키기 위한 중요한 기초 자료를 제공하며, 향후 정전기력에 의한 먼지 제거 효율을 최적화하기 위한 전극의 전압, 크기 및 위치 등의 설계를 개선할 수 있는 가능성을 제시한다.

References

Almuhanna, E.A., Maghirang, R.G., 2010. Measuring the electrostatic charge of airborne particles. Journal of Food, Agriculture & Environment, 8(3&4), 1033-1036.

Ansys, 2018. Ansys Fluent Documentation, ver 18.2. Ansys Inc., Canonsburg, PA, USA.

Carotenuto, C., Natale, F.D., Lancia, A., 2010. Wet electrostatic scrubbers for the abatement of submicronic particulate. Chemical Engineering Journal, 165, 35-45.

10.1016/j.cej.2010.08.049

Farnoosh, N., 2011. Three-dimensional modeling of electrostatic precipitator using hybrid finite element-flux corrected transport technique. PhD thesis in Electrical and Computer Engineering, The University of Western Ontario.

Geiling, T., Leopold, S., Cheriguen, Y., Hoffmann, M., 2012. Find dust measurement with electrical fields concept for a capacitive setup. Proceedings of the 23rd Micromechanics Europe Workshop, Ilmenau, Germany. 2012.

Jaworek, A., Adamiak, K., Balachandran, W., Krupa, A., Castle, P., Machowski, W., 2002. Numerical simulation of scavenging of small particles by charged droplets. Aerosol Science and Technology, 36, 913-924.

10.1080/02786820290092104

Jaworek, A., Balachandran, W., Krupa, A., Kulon, J., Lackowski, M., 2006. Wet electroscrubbers for state of the art gas cleaning. Environmental Science & Technology, 40(20), 6197-6207.

10.1021/es060592717120542

Manuzon, R.B., 2012. Electrostatic precipitation technologies for the mitigation of particulate matter emissions from poultry facilities. PhD thesis in Food, Agricultural and Biological Engineering, The Ohio State University, The United States.

Nielsen, N.F., Andersson, C., 2009. Electrode shape and collector plate spacing effects on ESP performance. In Electrostatic Precipitation: 11th International Conference on Electrostatic Precipitation, Hangzhou, 2008, Springer Berlin Heidelberg, 111-118.

10.1007/978-3-540-89251-9_23PMC3410458

Pilat, M.J., Jaasund, S.A., Sparks, L.E., 1974. Collection of aerosol particles by electrostatic droplet spray scrubbers, Environmental Science & Technology, 8(4), 360-362.

10.1021/es60089a006

Tan, Z., Zhang, Y., 2004. A review of effects and control methods of particulate matter in animal indoor environments. Journal of the Air & Waste Management Association, 54(7), 845-854.

10.1080/10473289.2004.1047095015303297

Wood, D.J., Van Heyst, B.J., 2016. A review of ammonia and particulate matter control strategies for poultry housing, Transactions of the ASABE, 59(1), 329-344.

10.13031/trans.59.10836

Ye, Q., Domnick, J., 2003. On the simulation of space charge in electrostatic powder coating with a corona spray gun. Powder Technology, 135, 250-260.

10.1016/j.powtec.2003.08.019

Journal of Animal Environmental Science ISSN:1226-0274(Print) 축산시설환경학회지

Preview

CFD simulation of wet electrostatic scrubbers for the mitigation of dust in livestock buildings

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

Figure 1.

Schematic model of the structure of WES (unit: m).

Figure 2.

Mesh generation on the plane at z=0.

Table 1.

Parameters for WES system.

Table 2.

Boundary conditions of CFD model.

Figure 3.

Collision detection through estimation of particle positions in 50 sub-time steps.

Figure 4.

Solution strategies for CFD simulations.

Table 3.

Simulation cases for WES performance test.

Figure 5.

Spatial distribution of electric potential, ion space charge and water droplets charged negatively by the electrode.

Table 4.

Dust removal performance according to the electrostatic forces.

Table 5.

Further investigation of dust removal performance with modified CFD simulations.

References